From the Medieval Research Blog: "The Quadrivium and the Stakes for Ordering the Mathematical Arts"

Legend has it that Pythagoras sentenced the first person to discover irrational numbers, Hippasus of Metapontum (c.530-450 BC), to death. He was tossed overboard a ship to drown. Why? Pythagoras taught that number was the essence and cause of all things, and for Pythagoras and his followers, numbers meant integers. Hippasus’ discovery of irrational numbers appeared to undermine the very core of Pythagoras’ teachings about the numerical nature of the universe. The secret could not get out. Hippasus had to die.

The existence of irrational numbers became a Pythagorean secret. They were called “unutterables” because in Greek, the ratio between two integers was called logos, and so, irrational numbers were called, alogos, which can be translated as either “irrational” or “not spoken.” The worry caused by this secret knowledge was somewhat alleviated by Eudoxus of Cnidos (408-355 BC) when he argued that the basis of reality was a ratio of magnitudes. In effect, Eudoxus made geometry replace arithmetic as the highest mathematical discipline, the foundation of all others. Geometry and arithmetic were hardly even separate disciplines at the time. This change of emphasis allowed Pythagorean teachings about the numeric nature of the universe to continue.

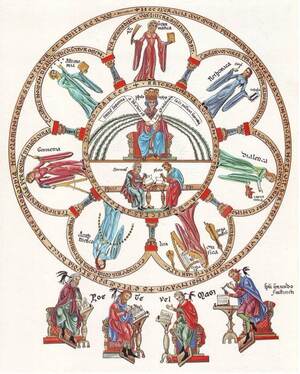
The idea that the mathematical disciplines have some orderly relationship between each other is essential for understanding the medieval concept of “quadrivium.” While it is well known that the medieval liberal arts curriculum, at least in its ideal established by Boethius, taught that a student must study both the trivium and quadrivium before progressing to philosophy and theology, the exact nature and rationale for the quadrivium is often less understood. Lists of the arts comprising the quadrivium (arithmetic, geometry, astronomy, and music/harmony) are consistent, but the exact order for these lists can vary. While there is no doubt that sometimes there is truly no rationale for a given order of the mathematical arts, attention to the mathematical art considered the principle or highest can reveal at least three identifiable streams of quadrivial traditions coming from the ancient world (similar to Chenu’s identification of different kinds of Platonism): the Boethian, the Calcidean, and the Capellan. The mathematical art considered “principle” is the one closest to metaphysical reality of the universe and serves as the foundation for all other mathematical disciplines. While the problem of irrational numbers may not have been on the forefront of anyone’s mind in the Middle Ages…it was a closely guarded Pythagorean secret after all…the problem of the principle mathematical art, inherited from Pythagoreanism, was readily available in the source texts.

This is an excerpt from "The Quadrivium and the Stakes for Ordering the Mathematical Arts" by Dr. Lesley-Anne Dyer Williams (LeTourneau University; MI Ph.D. '11). Read the full story.